Hình học là một loại toán rất thú vị và được nhiều nhà bác học nghiên cứu cho dù là quá hay hay hiện nay. Hôm nay mình sẽ hướng dẫn các bạn một trong những kiến thức nhỏ của hình học về đường tròn và tam giác, đó là cách tính bán kính đường tròn nội tiếp tam giác.
Hướng dẫn cách tính bán kính đường tròn nội tiếp tam có ví dụ cụ thể
Phương pháp giải: Sử dụng phương pháp diện tích tam giác
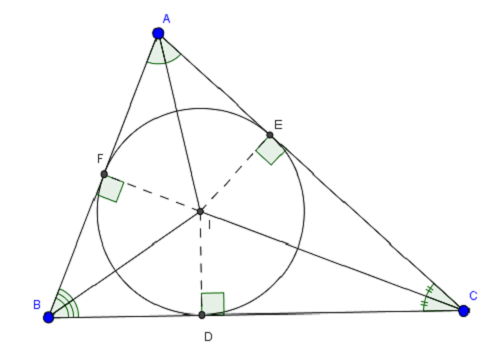
Cho tam giác ABC, ta có BC = a, CA = b và AB = c, r là bán kính đường tròn nội tiếp tam giác ABC, là nửa chu vi. Khi đó
Ví dụ cụ thể:
Ví dụ: Cho tam giác ABC, ta có AB = 6, AC = 7 và BC = 11. Hãy nêu cách tính bán kính đường tròn nội tiếp tam giác cụ thể.

Thế là bạn đã biết cách tính bán kính đường tròn nội tiếp tam giác, chúng thật dễ và đơn giản phải không nào.
Lý giải về hình học
Hình học là gì?
Hình học là một phần của toán học bao gồm các câu hỏi về hình dạng, kích thước, vị trí tương đối của các hình dạng và các tính chất không gian. Hình học được các nhà toán học phát triển độc lập trong một số nền văn hóa cổ đại như một phần của kiến thức thực tế về chiều dài, diện tích và thể tích, và một số yếu tố của toán học đến từ phương Tây. chẳng hạn như những tuyên bố của Thales (thế kỷ 6 trước Công nguyên).

Trong thế kỷ thứ 3 trước Công nguyên, hình học của Euclid đã được hệ thống hóa dưới dạng tiên đề với tên của ông. Hình học Euclid đã trở thành chuẩn mực trong nhiều thế kỷ. Archimedes đã phát triển các kỹ thuật tiên tiến để tính diện tích và khối lượng theo cách áp dụng phép tính tích phân. Thiên văn học đã trở thành nguồn chính của các vấn đề trong hình học trong suốt hơn 1.500 năm tới khi tính toán vị trí của các ngôi sao và hành tinh trên bản đồ thiên thể và mô tả mối quan hệ giữa chuyển động của các thiên thể. Trong thế giới cổ điển, cả hình học và thiên văn học đều được coi là một phần của quadrivium, là một phần của bảy lĩnh vực giáo dục tự do mà mọi công dân phải nắm vững.
Hình học trong lịch sử
René Descartes đưa ra hệ tọa độ và sự phát triển đồng thời của đại số đã đánh dấu một giai đoạn mới trong sự phát triển của hình học, vì hình học như đường cong phẳng không thể được mô tả giải tích. dưới dạng phương trình và hàm số. Điều này đóng một vai trò quan trọng trong sự phát triển của phép tính tích phân trong thế kỷ 17. Sau đó, lý thuyết phối cảnh đã chỉ ra rằng có nhiều yếu tố hình học hơn chỉ là các thuộc tính số của các mẫu: phối cảnh đã trở thành một nguồn của hình học xạ ảnh. Các đối tượng nghiên cứu hình học được mở rộng hơn nữa bằng cách nghiên cứu cấu trúc bên trong của các đối tượng hình học Euler và Gauss, dẫn đến sự hình thành các nhánh tôpô và vi phân.

Trong thời kỳ Euclid, không có sự phân biệt rõ ràng giữa không gian vật lý và hình học. Kể từ khi hình học phi Euclide được phát hiện vào thế kỷ 19, các khái niệm về không gian đã thay đổi hoàn toàn, đặt ra câu hỏi về không gian nào phù hợp nhất với không gian vật lý. Với sự phát triển của toán học lý thuyết trong thế kỷ 20, ‘không gian’ (dù là ‘điểm’, ‘đường thẳng’ hay ‘mặt phẳng’) mất đi nội dung trực quan của nó, vì vậy người đọc phải phân biệt giữa không gian vật lý và không gian hình học (ở đâu) ‘không gian’ , ‘point’, v.v. Nó vẫn có ý nghĩa trực quan) và không gian trừu tượng. Hình học hiện đại coi không gian là linh hoạt – không gian có mức độ trừu tượng cao hơn nhiều so với không gian Euclid thông thường. Hình học có nhiều mối quan hệ với vật lý, thể hiện qua mối quan hệ của Riemann giữa hình học và thuyết tương đối rộng Một trong những lý thuyết mới nhất trong vật lý, lý thuyết dây, cũng rất gần với hình học.
Có thể thấy là hình học có 3 loại chính được phát hiện từ trước đến nay, bao gồm: Hình học Euclid, hình học Lobachewski, và hình học Riemann. Nhưng phần lớn chúng ta chỉ áp dụng hình học Euclid là nhiều. Vậy hình học Euclid là gì? Hình học trường học, trong đó các hình vẽ và sơ đồ được vẽ trên giấy hoặc bảng đen trơn, được gọi là hình học Euclid để vinh danh nhà toán học Euclid. Ông đã kết hợp tất cả những kiến thức hình học mà ông từng có được thành một dạng có hệ thống và logic và biên soạn nó thành 13 phần gọi là “Các phần tử”.
Kết luận
Qua bài viết này mong bạn có thể hiểu rõ hơn về hình học thú vị này. Có thể nói chúng không bao giờ có điểm kết, vì thế chúng ta có thể học tập được rất nhiều từ nó. Và cách tính bán kính đường tròn nội tiếp tam giác – là một trong những kiến thức đơn giản của ngày hôm nay là kiến thức đang để chúng ta ghi nhớ.






























